User Guide
Median
The median, like the average, represents the position of the distribution in the space of real numbers.
Median meis the number that separates the ordered series into two groups of the same number.
To determine it, we write the list of all the values of the series in ascending order, each one repeated as many times as its number.
If the total number n is an odd number, the median is the term in the row .
If total staff complement s is an even number, the median is the center of the interval formed from the terms in the row and .
For a normal distribution
Why use the median:
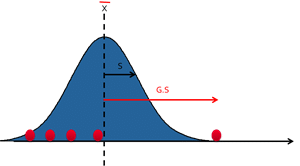
To be less sensitive to abnormal values
 .
.

The average calculation is given by:
It is thus sensitive to abnormal data as a distant value will have a lot of weight. For the calculation to be less sensitive to this kind of data, we prefer to use the median.
When the distribution is not symmetrical
When the data distribution is not symmetrical (for example, salary distribution in France), using the average would have little interest as it would be strongly pulled to one side or the tail of the distribution would be elongated.
In this case we prefer to use the median, which best defines the position of the curve in the space of real numbers;
It actually better corresponds to our intuitive definition of the position of the curve. To understand this, let us take the following example: which value corresponds the best to the position of the curve in the following example: