Ellistat logo
Descriptive statistics
Statistical tests
Design of Experiment
Gage RR
Problem resolution
Reliability
Control plan
User's Guide Menu

User Guide

Statistical test power

The power of a test corresponds to the capacity of a statistical test to detect a difference. The higher the power the higher the probabiilty that the test will detect a difference.
To calculate a tests power, choose the test that you want to use:
  • z theoretical: compare a sample average with a theoretical value provided that you already know the population's standard deviation
  • t theoretical: compare a sample average with a theoretical value without knowing the population's standard deviation. This will be calculated based on the test sample
  • t Test: compare the average of two samples
  • Paired t test: compares the average of two samples by comparing data in pairs (2 by 2)
  • Chi2: compares the standard deviation of a sample based on a theoretical value
  • F Test : compares the standard deviations of two samples
  • Test 1P: compares the proportion obtained from a sample (Ex: 3 defects out of 1000 parts) based on a theoretical proportion
  • Test 2P: compares 2 proportions measured from two different samples (Ex: Batch A: 2 defects out of 24, Lot B: 4 defects out of 26)
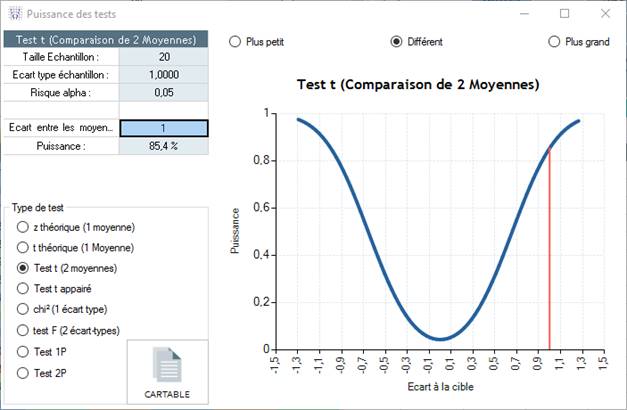
    Puissance d'un test statistique
Then enter:
  • The sample size that you want to use
  • The expected standard deviation for your values. This standard deviation can be an estimate, for example:
  • We know that the temperature varies ± 4° for normal production (expert estimate). We believe that this estimate covers 95% of the actual dispersion (± 4 sigma) so we estimate the residual standard deviation as 1.
  • The alpha risk from which you will conclude that the difference is significant: generally it is advised to leave it at 0.05.
  • The typical difference that you want to evaluate: in the preceding example we want to observe an average difference of 1 between the 2 samples.
Ellistat will then give you the test's power which is 85.4% in this example. This means: If the difference between the two averages equals 1, then the test t will have an 85.4% chance of detecting a significant difference between the samples.
On the other hand, if you want to determine the number of samples necessary to get a given power, all you have to do is enter the desired power in the corresponding box and Ellistat will automatically calculate the number of samples you need to obtain the given power.