Ellistat logo
Descriptive statistics
Statistical tests
Design of Experiment
Gage RR
Problem resolution
Reliability
Control plan
User's Guide Menu

User Guide

Weibull distribution

In order to create a model of the failure distribution of a product, it is necessary to be able to model multiple types of failure:
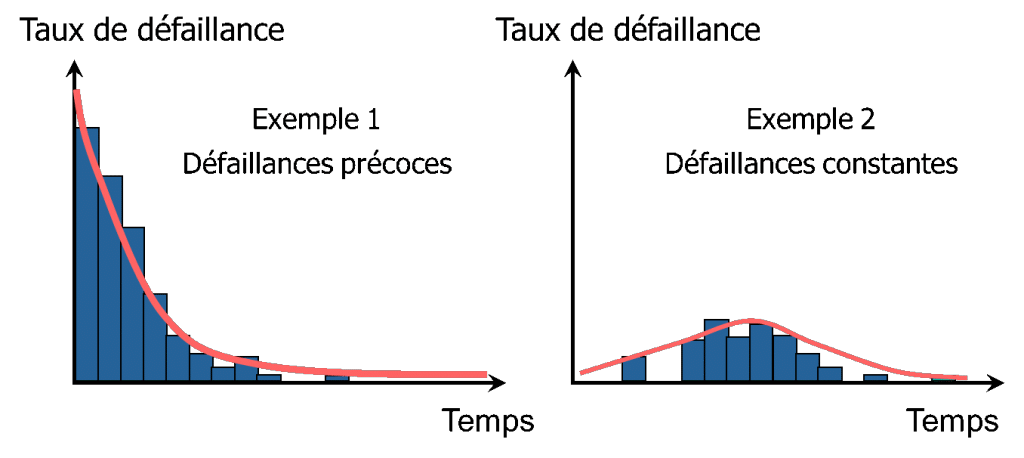
Exemple de loi
Therefore, considerable shape flexibility is necessary. The distribution primarily used for this is the Weibull distribution because it allows for a greater shape variability.
Because of its flexibility, the Weibull distribution makes the modelling of the behaviour of numerous types of failure possible, such as
  • Components' resistance to rupture or the effort required to wear out metals.
  • The failure time of an electronic component.
  • The failure time for articles used outdoors such as pneumatic automobiles.
  • Systems that fail when the weakest component in the system contains a defect. The Weibull distribution also supports the modelling of the behaviour of different lifespan situations for one component. The function of the Weibull distribution is as follows:
It is composed of 3 parameters:
  • β - shape parameter
  • θ - scale parameter
  • δ - delay parameter

β, shape parameter :

It makes adaptation of the distribution's shape possible to place it as close as possible to the observed failure rate:
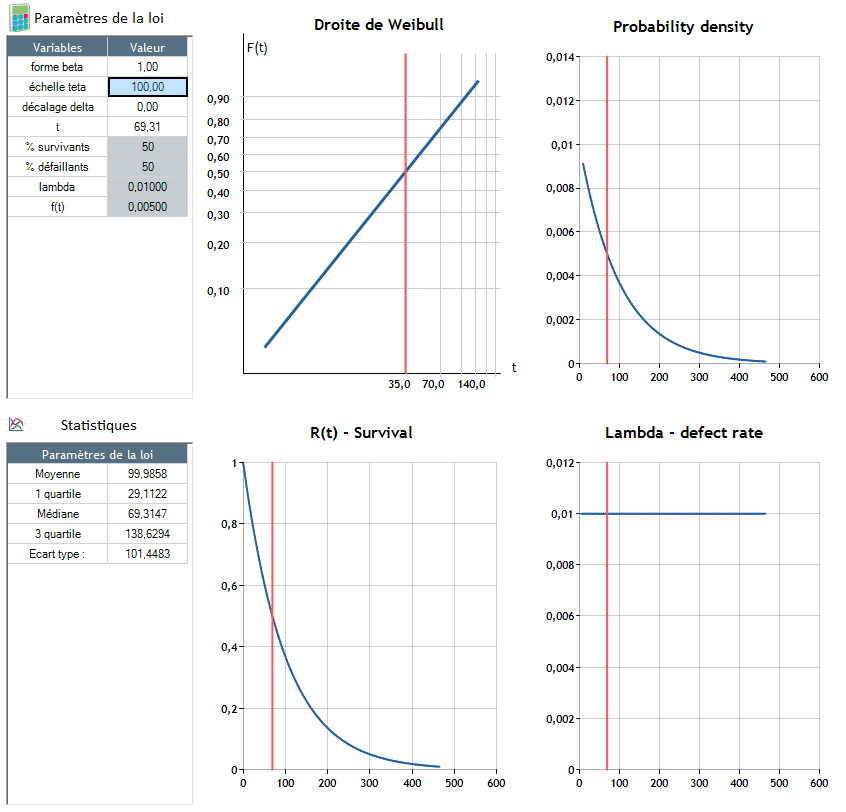
Wiebull beta = 1
β = 1: The failure rate is constant (λ constant)
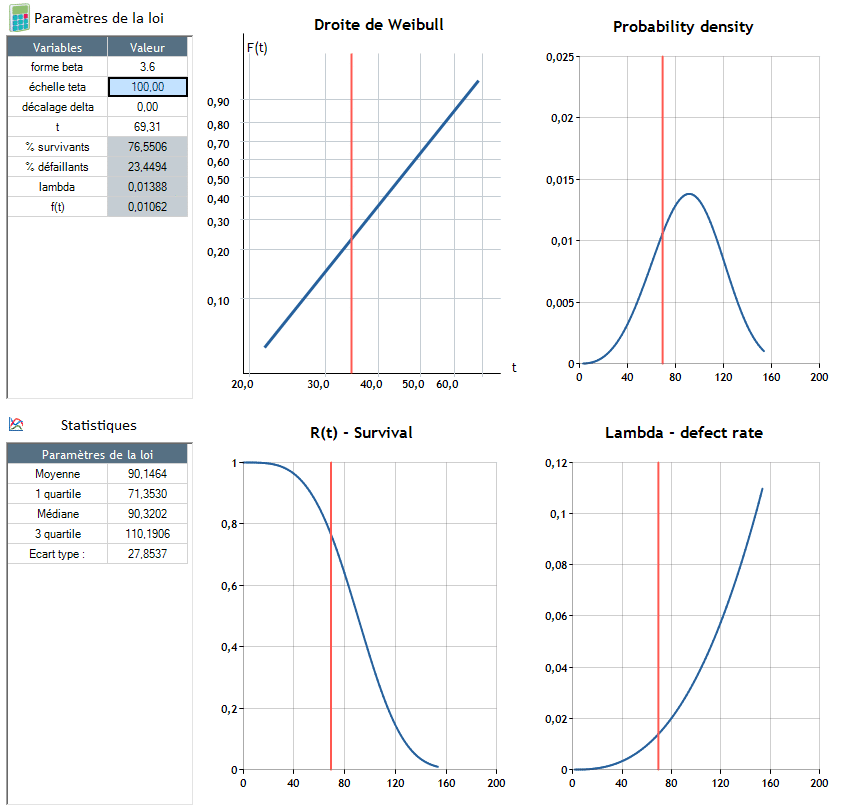
wiebull beta = 2.6
β > 1: The failure rate increases with time (λ increases - product's end of life)
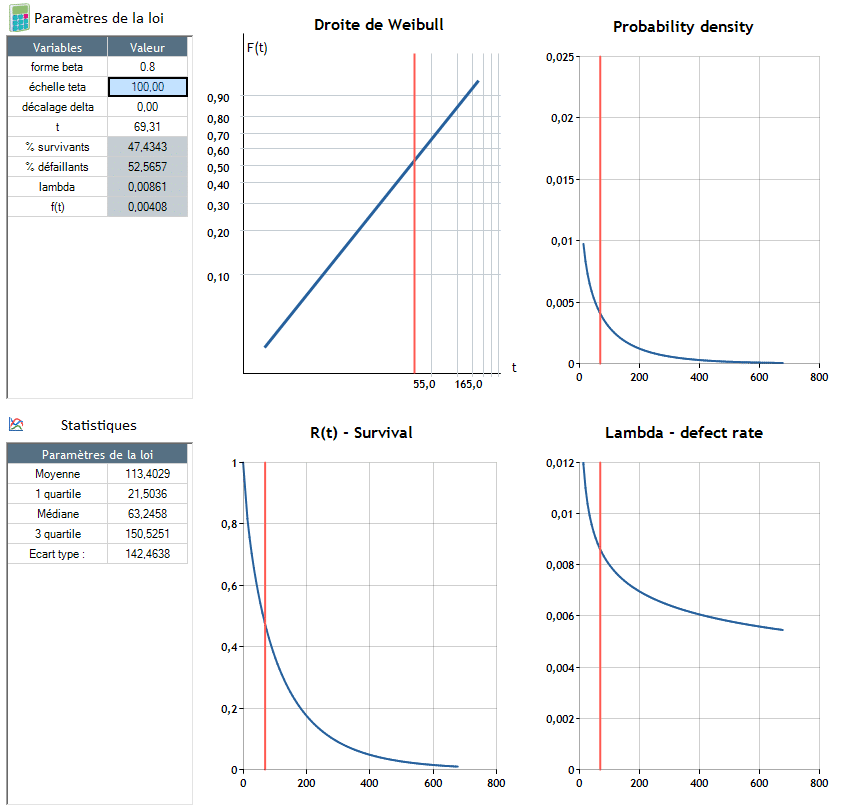
Weibull beta = 0.8
β < 1: The failure rate decreases with time (λ decreases - infant failure)

θ, scale parameter :

The θ parameter makes it possible to adjust the scale of the distribution law to the scale of the observed problem, for example:
wiebull beta = 2.6
Failure appears around t = 90.4
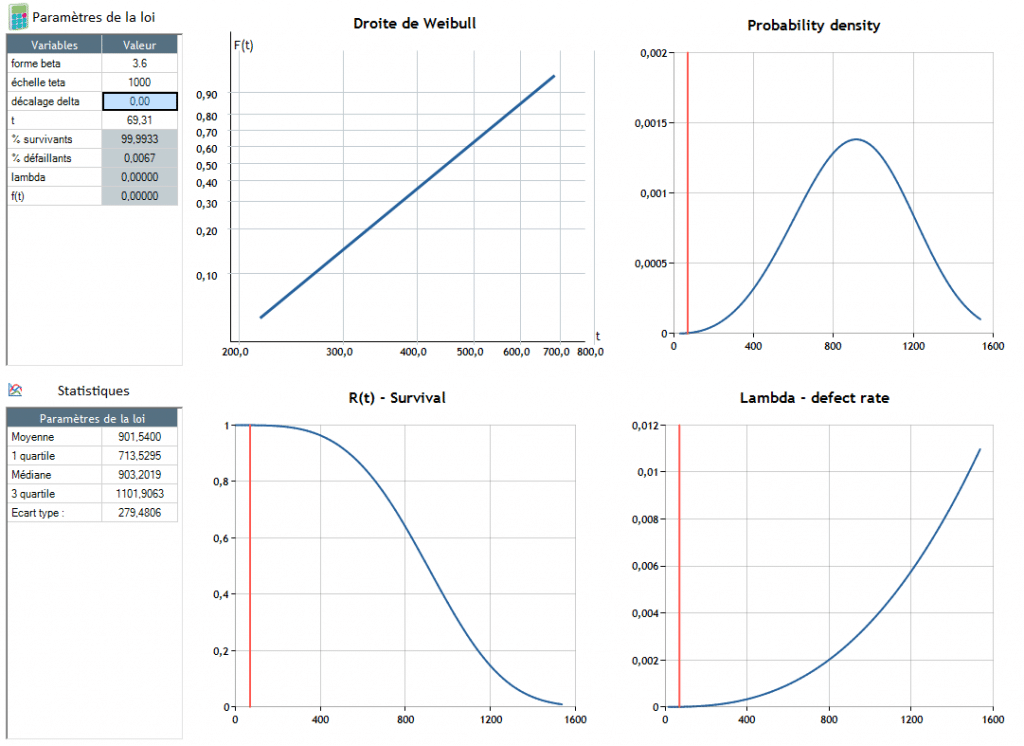
Wiebull theta = 1000
Failure appears around t = 904

δ, delay parameter:

The δ parameter makes it possible to move the distribution law by one parameter δ
wiebull beta = 2.6
Β = 3,6 – θ = 100, δ = 0
Failure appears around t = 90.4
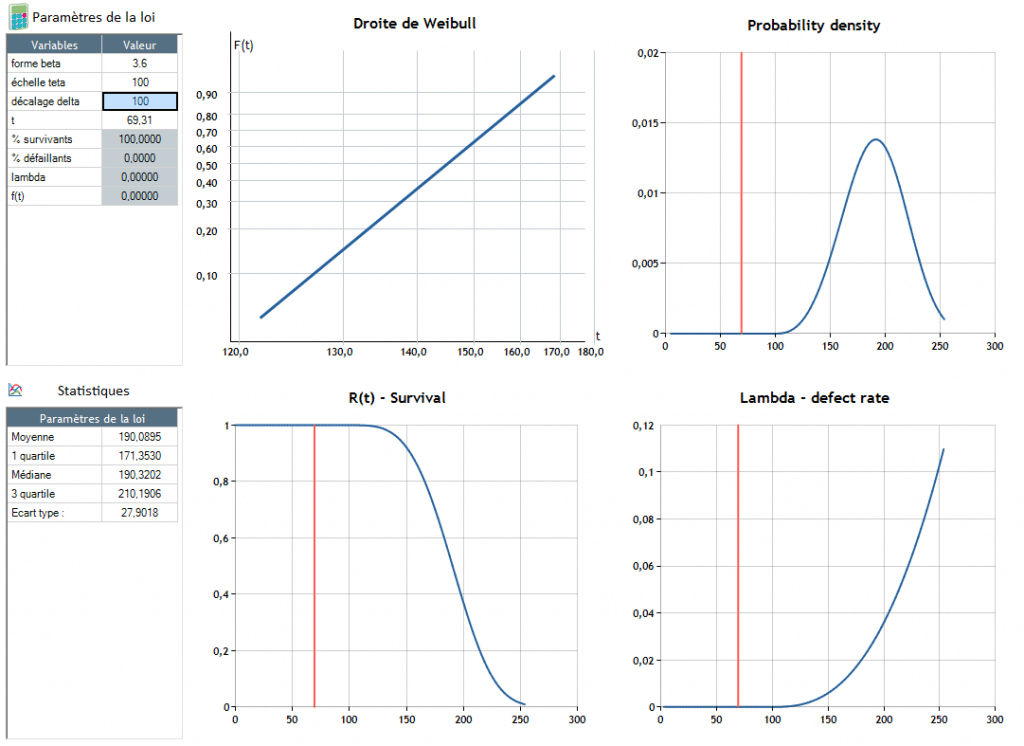
Weibull delta = 100
Β = 3,6 – θ = 100, δ = 100
Failure appears around t = 190.4